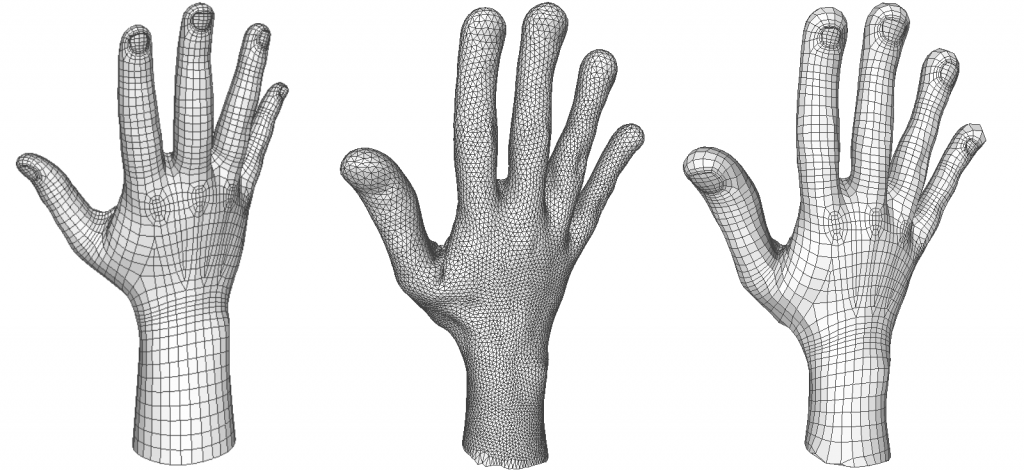
Reversible Harmonic Maps
Danielle Ezuz, Justin Solomon and Mirela Ben-Chen
ACM Transactions on Graphics (TOG), to be presented at SIGGRAPH 2019
Paper
ABSTRACT: Information transfer between triangle meshes is of great importance in computer graphics and geometry processing. To facilitate this process, a smooth and accurate map is typically required between the two meshes. While such maps can sometimes be computed between nearly-isometric meshes, the more general case of meshes with diverse geometries remains challenging. We propose a novel approach for direct map computation between triangle meshes without mapping to an intermediate domain, which optimizes for the harmonicity and reversibility of the forward and backward maps. Our method is general both in the information it can receive as input, e.g. point landmarks, a dense map or a functional map, and in the diversity of the geometries to which it can be applied. We demonstrate that our maps exhibit lower conformal distortion than the state-of-the-art, while succeeding in correctly mapping key features of the input shapes.

Elastic Correspondence between Triangle Meshes
Danielle Ezuz, Behrend Heeren, Omri Azencot, Martin Rumpf and Mirela Ben-Chen
Computer Graphics Forum, Eurographics 2019
Paper
ABSTRACT: We propose a novel approach for shape matching between triangular meshes that, in contrast to existing methods, can match crease features. Our approach is based on a hybrid optimization scheme, that solves simultaneously for an elastic deformation of the source and its projection on the target. The elastic energy we minimize is invariant to rigid body motions, and its non-linear membrane energy component favors locally injective maps. Symmetrizing this model enables feature aligned correspondences even for non-isometric meshes. We demonstrate the advantage of our approach over state of the art methods on isometric and non-isometric datasets, where we improve the geodesic distance from the ground truth, the conformal and area distortions, and the mismatch of the mean curvature functions.
Finally, we show that our computed maps are applicable for surface interpolation, consistent cross-field computation, and consistent quadrangular remeshing of a set of shapes.
Finally, we show that our computed maps are applicable for surface interpolation, consistent cross-field computation, and consistent quadrangular remeshing of a set of shapes.
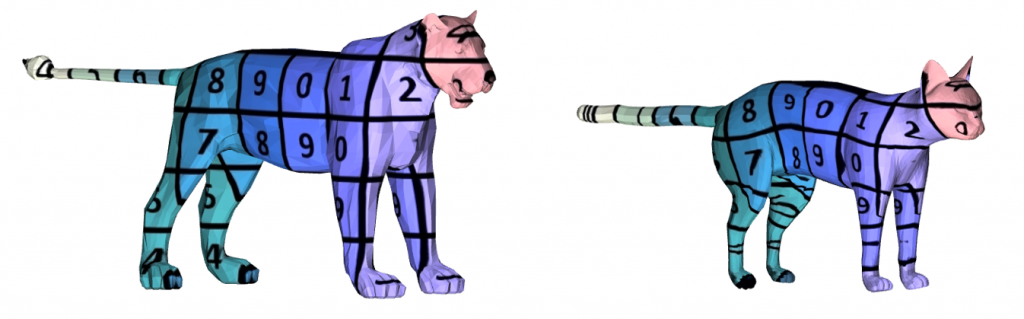
A Genetic Algorithm for Fully Automatic Non-Isometric Shape Matching
Michal Edelstein, Danielle Ezuz and Mirela Ben-Chen
Paper
ABSTRACT: Automatically computing shape correspondence is a difficult problem, especially when the shapes are significantly different. In this paper we suggest a fully automatic method for shape correspondence, that is suitable for non isometric shapes and shapes of different topology. We tackle the combinatorial task of putting in correspondence two sparse sets of landmarks using a genetic algorithm. Our main observation is that optimizing an objective based on an induced dense functional correspondence, combined with geometric genetic operators, is highly effective for non isometric shape matching. The output of the genetic algorithm is a sparse landmark correspondence, as well as a corresponding functional map. Finally, an accurate pointwise map is extracted using existing semi-automatic methods. Our method is general, widely applicable, and outperforms state of the art methods for automatic shape correspondence both quantitatively and qualitatively.
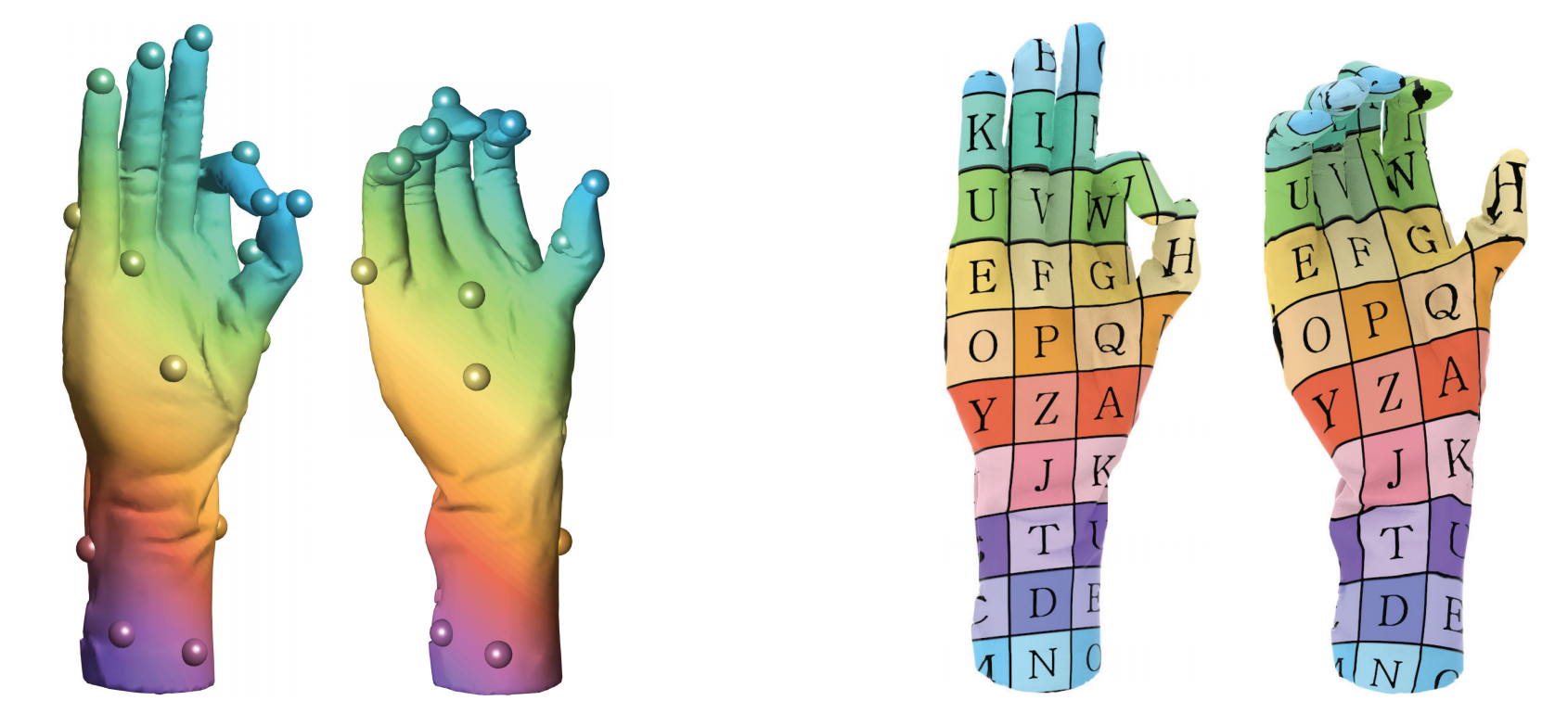
Deblurring and Denoising of Maps between Shapes
Danielle Ezuz and Mirela Ben-Chen
Computer Graphics Forum, SGP 2017
Paper | Code
ABSTRACT: Shape correspondence is an important and challenging problem in geometry processing. Generalized map representations, such as functional maps, have been recently suggested as an approach for handling difficult mapping problems, such as partial matching and matching shapes with high genus, within a generic framework.
While this idea was shown to be useful in various scenarios, such maps only provide low frequency information on the correspondence. In many applications, such as texture transfer and shape interpolation, a high quality pointwise map that can transport high frequency data between the shapes is required. We name this problem map deblurring and propose a robust method, based on a smoothness assumption, for its solution. Our approach is suitable for non-isometric shapes, is robust to mesh tessellation and accurately recovers vertex-to-point, or precise, maps. Using the same framework we can also handle map denoising, namely improvement of given pointwise maps from various sources. We demonstrate that our approach outperforms the state-of-the-art for both deblurring and denoising of maps on benchmarks of non-isometric shapes, and show an application to high quality intrinsic symmetry computation.
While this idea was shown to be useful in various scenarios, such maps only provide low frequency information on the correspondence. In many applications, such as texture transfer and shape interpolation, a high quality pointwise map that can transport high frequency data between the shapes is required. We name this problem map deblurring and propose a robust method, based on a smoothness assumption, for its solution. Our approach is suitable for non-isometric shapes, is robust to mesh tessellation and accurately recovers vertex-to-point, or precise, maps. Using the same framework we can also handle map denoising, namely improvement of given pointwise maps from various sources. We demonstrate that our approach outperforms the state-of-the-art for both deblurring and denoising of maps on benchmarks of non-isometric shapes, and show an application to high quality intrinsic symmetry computation.
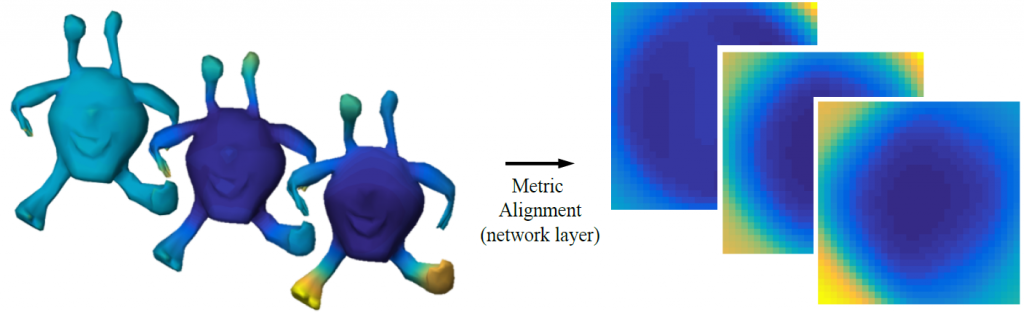
GWCNN: A Metric Alignment Layer for Deep Shape Analysis
Danielle Ezuz, Justin Solomon, Vladimir Kim and Mirela Ben-Chen
Computer Graphics Forum, SGP 2017
Paper
ABSTRACT: Deep neural networks provide a promising tool for incorporating semantic information in geometry processing applications.
Unlike image and video processing, however, geometry processing requires handling unstructured geometric data, and thus data representation becomes an important challenge in this framework. Existing approaches tackle this challenge by converting point clouds, meshes, or polygon soups into regular representations using, e.g., multi-view images, volumetric grids or planar parameterizations. In each of these cases, geometric data representation is treated as a fixed pre-process that is largely disconnected from the machine learning tool. In contrast, we propose to optimize for the geometric representation during the network learning process using a novel metric alignment layer. Our approach maps unstructured geometric data to a regular domain by minimizing the metric distortion of the map using the regularized Gromov–Wasserstein objective. This objective is parameterized by the metric of the target domain and is differentiable; thus, it can be easily incorporated into a deep network framework. Furthermore, the objective aims to align the metrics of the input and output domains, promoting consistent output for similar shapes. We show the effectiveness of our layer within a deep network trained for shape classification, demonstrating state-of-the-art performance for nonrigid shapes.
Unlike image and video processing, however, geometry processing requires handling unstructured geometric data, and thus data representation becomes an important challenge in this framework. Existing approaches tackle this challenge by converting point clouds, meshes, or polygon soups into regular representations using, e.g., multi-view images, volumetric grids or planar parameterizations. In each of these cases, geometric data representation is treated as a fixed pre-process that is largely disconnected from the machine learning tool. In contrast, we propose to optimize for the geometric representation during the network learning process using a novel metric alignment layer. Our approach maps unstructured geometric data to a regular domain by minimizing the metric distortion of the map using the regularized Gromov–Wasserstein objective. This objective is parameterized by the metric of the target domain and is differentiable; thus, it can be easily incorporated into a deep network framework. Furthermore, the objective aims to align the metrics of the input and output domains, promoting consistent output for similar shapes. We show the effectiveness of our layer within a deep network trained for shape classification, demonstrating state-of-the-art performance for nonrigid shapes.